T1 题意:你要进行n次操作,第i次选择一个数k∈[1,i],并插入到当前序列的第k个位置。给定目标序列,输出操作序列。100,2s。
解:冷静分析一波,我们可以从后往前确定操作序列。这样每次确定一个操作之后就会删除一个数。
如果有ai = i的位置那我们显然可以把这个i操作放到操作序列最后。如果有多个这样的i,从后往前处理。


1 #include2 3 const int N = 110; 4 5 int a[N], b[N]; 6 7 int main() { 8 9 int n;10 scanf("%d", &n);11 for(int i = 1; i <= n; i++) {12 scanf("%d", &b[i]);13 }14 for(int i = n; i >= 1; i--) {15 bool f = 0;16 for(int j = i; j >= 1; j--) {17 if(b[j] > j) break;18 if(b[j] == j) {19 a[i] = j;20 //printf("a %d = %d \n", i, j);21 for(int k = j; k < i; k++) {22 b[k] = b[k + 1];23 }24 f = 1;25 break;26 }27 }28 if(!f) {29 printf("-1");30 return 0;31 }32 }33 for(int i = 1; i <= n; i++) {34 printf("%d\n", a[i]);35 }36 return 0;37 }
T2 题意:构建一个n个点的简单无向连通图,使得每个点的邻居的编号之和相等。100,2s。
解:先玩一下3和4的时候,发现是一张完全二分图,且左右部的节点编号之和相等。
这启发我们把这些点分成k份,每份的编号之和相同。然后每个点向其他所有不是同类的点连边。
n为偶数的时候就是首尾配对,和为n + 1,n为奇数的时候提出n来然后首尾配对,和为n。


1 #include2 3 const int N = 110; 4 5 int vis[N]; 6 7 int main() { 8 9 int n, cnt1 = 0;10 scanf("%d", &n);11 int t = (n + 1) * n / 2;12 if(t & 1) {13 if((n & 1) == 0) {14 printf("%d\n", n * (n - 2) / 2);15 for(int i = 1; i <= n; i++) {16 for(int j = i + 1; j <= n; j++) {17 if(i + j != n + 1) {18 printf("%d %d \n", i, j);19 }20 }21 }22 return 0;23 }24 else {25 printf("%d \n", (n - 1) * (n - 3) / 2 + n - 1);26 for(int i = 1; i < n; i++) {27 printf("%d %d \n", i, n);28 }29 for(int i = 1; i < n; i++) {30 for(int j = i + 1; j < n; j++) {31 if(i + j != n) {32 printf("%d %d \n", i, j);33 }34 }35 }36 }37 return 0;38 }39 t /= 2;40 for(int i = n; i >= 1 && t; i--) {41 if(t >= i) {42 t -= i;43 vis[i] = 1;44 cnt1++;45 }46 }47 printf("%d\n", cnt1 * (n - cnt1));48 for(int i = 1; i <= n; i++) {49 if(vis[i]) {50 for(int j = 1; j <= n; j++) {51 if(!vis[j]) {52 printf("%d %d \n", i, j);53 }54 }55 }56 }57 58 return 0;59 }
T3 题意:给定简单无向连通图,问是否能把所有边分成三个环。点可以重复经过。10w,10w,2s。
解:这TM居然是分类讨论...首先有度数为奇的肯定不行。然后只要排除一种情况:总环数 < 3即可。
因为如果环比较多,任意两个相邻(共用某一点)的环肯定能合二为一的......
如果有某个点的度数大于4,肯定合法。如果没有点的度数大于2,肯定不合法。
当点的度数最大为4的时候,可以把其他所有度数为2的点缩成某些边。
如果只有一个点的度数为4,相当于该点有两条自环,不行。
如果有两个点的度数为4,有一种特殊情况不合法:
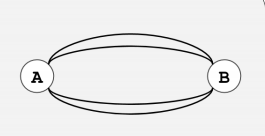
其余情况和有大于2个点的度数等于4的时候,均合法。


1 #include2 3 const int N = 100010; 4 5 struct Edge { 6 int nex, v; 7 }edge[N << 1]; int tp = 1; 8 9 int e[N], n, m, in[N], vis[N], stk[N], top, cnt, A, B;10 11 inline void add(int x, int y) {12 tp++;13 edge[tp].v = y;14 edge[tp].nex = e[x];15 e[x] = tp;16 return;17 }18 19 void DFS(int x, int f) {20 if(f && x == A) {21 puts("Yes");22 exit(0);23 }24 else if(x == B) return;25 for(int i = e[x]; i; i = edge[i].nex) {26 int y = edge[i].v;27 if(y != f) DFS(y, x);28 }29 return;30 }31 32 int main() {33 scanf("%d%d", &n, &m);34 for(int i = 1, x, y; i <= m; i++) {35 scanf("%d%d", &x, &y);36 add(x, y);37 add(y, x);38 in[x]++;39 in[y]++;40 }41 int largeIn = 0, cnt = 0;42 for(int i = 1; i <= n; i++) {43 if(in[i] & 1) {44 puts("No");45 return 0;46 }47 if(largeIn < in[i]) {48 largeIn = in[i];49 cnt = 1;50 }51 else if(largeIn == in[i]) {52 cnt++;53 }54 }55 if(largeIn > 4) {56 puts("Yes");57 return 0;58 }59 else if(largeIn == 4 && cnt > 2) {60 puts("Yes");61 return 0;62 }63 else if(largeIn == 4 && cnt == 2) {64 for(int i = 1; i <= n; i++) {65 if(in[i] == 4) {66 if(!A) A = i;67 else {68 B = i;69 break;70 }71 }72 }73 DFS(A, 0);74 }75 puts("No");76 return 0;77 }
T4 题意:给定一个排列。你可以花费A使一个区间最左边的数跑到最右边,其余区间内的数左移。也可以花费B来进行逆操作。求使其变成升序的最小代价。5000,2s。
解:神仙DP。
显然有个n3的区间DP是设f[l][r]表示把[l, r]这一段排序。转移的时候一段区间可以由两个子区间拼起来,也可以找到其中最值然后挪一次。
正解全然不同......我们只注重这些元素的相对位置,也就是说下标可以为实数。
然后考虑每次操作等价于把一个数往旁边挪,别的数不变。
然后考虑最优解肯定是若干个数往左,若干个数往右,若干个数不动。我们以那些不动的数来DP。
设f[i][j]表示值域前i个数全部排好序了,且最大的那个不动的数是j,且比j大的数全部聚集在(j, j + 1)这一段的最小代价。
考虑f[i][j]是怎么得来的:如果当前这个数i初始时在j的左边,那么一定要往右移(i比j大)。反之一定要往左移(聚集到(j, j + 1)中)。
然后我们忽了一种转移:i在j右边的时候也可以不移动!此时f[i][i] = f[i - 1][j]
然后就完事了。


1 #include2 3 typedef long long LL; 4 const int N = 5010; 5 6 LL f[N][N]; 7 int a[N], p[N]; 8 9 int main() {10 11 int n;12 LL A, B;13 scanf("%d%lld%lld", &n, &A, &B);14 for(int i = 1; i <= n; i++) {15 scanf("%d", &a[i]);16 p[a[i]] = i;17 }18 memset(f, 0x3f, sizeof(f));19 /// DP20 f[0][0] = 0;21 for(int i = 1; i <= n; i++) {22 for(int j = 0; j < i; j++) {23 /// f[i][j]24 /*for(int k = 0; k < i; k++) {25 /// f[i][j] <- f[i - 1][k]26 if(p[i] < p[k]) {27 f[i][j] = std::min(f[i][j], f[i - 1][k] + A);28 }29 else {30 f[i][j] = std::min(f[i][j], f[i - 1][k] + B);31 }32 }*/33 if(p[i] < p[j]) {34 f[i][j] = f[i - 1][j] + A;35 }36 else {37 f[i][j] = f[i - 1][j] + B;38 f[i][i] = std::min(f[i][i], f[i - 1][j]);39 }40 }41 /*for(int j = 0; j <= i; j++) {42 printf("%3lld ", f[i][j]);43 }44 puts("");*/45 }46 47 48 LL ans = 4e18;49 for(int i = 0; i <= n; i++) {50 ans = std::min(ans, f[n][i]);51 }52 printf("%lld\n", ans);53 return 0;54 }
T5 题意:给定序列,把它们两两配对使得每一对的和 % MO的最大值最小。10w,1e9,2s。
解:排序之后考虑最优方案长什么样。
然后发现它们一定长这样...因为不满足这样的方案调整成这样一定更优。
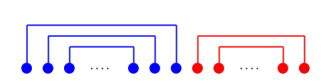
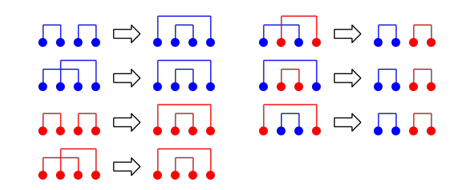
枚举分界点是n2的,但是发现分界点越靠左越优,于是二分这个分界点,使其满足条件(左边的和全小于MO,右边全不小于MO),然后一次得出答案。
单调性:就考虑若分界点在a和b都满足条件,那么a,b之间的任一点也满足条件。比b小所以左边满足,比a大所以右边满足。


1 #include2 3 const int N = 200010; 4 5 int a[N], MO, n; 6 7 inline bool check(int p) { 8 int l = p + 1, r = n; 9 while(l < r) {10 if(a[l] + a[r] < MO) return false;11 l++;12 r--;13 }14 return true;15 }16 17 int main() {18 scanf("%d%d", &n, &MO);19 n <<= 1;20 for(int i = 1; i <= n; i++) {21 scanf("%d", &a[i]);22 }23 std::sort(a + 1, a + n + 1);24 25 int l = n, r = n; /// [1, l] (l, r]26 while(a[n] + a[l - 1] >= MO && l >= 2) l -= 2;27 while(a[1] + a[r] >= MO && r >= 2) r -= 2;28 l /= 2;29 r /= 2;30 31 while(l < r) {32 int mid = (l + r) >> 1;33 if(check(mid * 2)) r = mid;34 else l = mid + 1;35 }36 37 int p = r * 2;38 int ans = 0;39 l = 1, r = p;40 while(l < r) {41 ans = std::max(ans, a[l] + a[r]);42 l++;43 r--;44 }45 l = p + 1, r = n;46 while(l < r) {47 ans = std::max(ans, (a[l] + a[r]) % MO);48 l++;49 r--;50 }51 printf("%d\n", ans);52 return 0;53 }